2.3: Dividir en dos

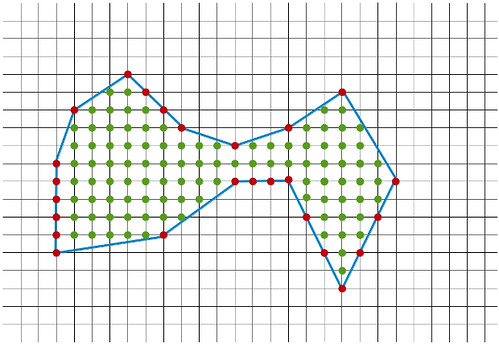
En este desafío vacacional, se trata de conseguir dividir en dos partes (iguales en la forma y en el área) cada una de las piezas que aparecen en esta construcción de Geogebra.
 Están extraídas del mes de enero de 2016 del calendario matemático que tienes en el menú lateral. Para trabajar de forma más cómoda, en ventana más grande, puedes hacerlo desde este enlace.



Sobre este applet, puedes ir probando diferentes formas, utilizando la herramienta Lápiz que tienes disponible. Para borrar el trazo hay que hacer clic en el botón derecho y el cursor se volverá una goma de borrar.

El desafío para estas vacaciones es intentar conseguir resolver todos los que puedas. Para hacerlos llegar basta que hagas una captura de pantalla y me la envíes por correo electrónico.

2.2: Ordenando números

Problema del día 11 de diciembre del calendario que tienes en el margen.

Como verás, la calculadora no tiene tanta potencia de cálculo y te dará errores. Entonces hay que pensar alguna estrategia que te permita resolverlo. Es posible que haya otras, pero por si no te ocurre cómo atacar el problema, te sugiero que pienses en el máximo común divisor de los exponentes.

2.1: Refranes

Te propongo dibujar gráficas partiendo del significado de refranes. Debes indicar claramente qué se representa en cada eje y la escala. Aquí tienes un ejemplo:

· Refrán: EL HAMBRE AGUDIZA EL INGENIO

· Magnitudes que se relacionan: nivel de ingenio y nivel de hartazgo.
· Variable independiente: nivel de hartazgo. Se ”mide” en % en una escala de 0 a 100
· Variable dependiente: nivel de ingenio. Se “mide” mediante una escala subjetiva (poco, bastante, mucho…)
· Representación gráfica:

Ahora te toca a ti. Elige un refrán que conozcas  que relacione dos variable y represéntalo gráficamente siguiendo el esquema del ejemplo.

1.11: Triángulo y círculo

1.10: Contenedores

Problema del día 7 de noviembre del calendario matemático enlazado en este blog

1.9: Puzzle geométrico

Soluciones al problemas de los cordones

Han llegado 5 soluciones. Os pongo aquí tres de ellas, abordadas desde formas distintas, algebraica y numéricamente.

1.8: Mosaico

El desafío de esta semana está dirigido a la búsqueda de mosaicos en tu vida cotidiana. ¿Qué condiciones ha de cumplir?
- Que se pueda extender a todo el plano
- Que las figuras no se solapen y todo quede recubierto utilizando el mismo tipo de piezas.
¿En que consiste el desafío? En localizar uno o más mosaicos en tu entorno, hacer una foto y explicar cuál es la pieza base con la que se consigue el mosaico.
¿Qué se valora? El cumplimiento de los requisitos y la originalidad de las piezas. NO VALE buscar en internet, ha de estar en fachadas, suelos, calle, etc.

Suelo de la glorieta de Santa Orosia, en Calamocha

1.7: Cordones

Problema del día 2 de noviembre del calendario matemático enlazado en este blog

Soluciones a las velas

He recibido dos formas distintas de solucionar el problema de las velas. Una utilizando el álgebra y la otra las funciones. Muy bien en ambos casos.

1.6: What's the probability?

What is the probability that four different points chosen at random from the fifteen equally spaced points shown are the vertices of a square? Express your answer as a common fraction.

1.5: Medir áreas con puntos

Esta semana la propuesta es leer el artículo que te enlazo y contestar a lo que se plantea en él. Al leerlo te darás cuenta de que te ofrece la manera de resolverlo. Anímate.

Soluciones anteriores

Aunque un poco tarde, aquí os pongo las soluciones que me habéis ido dando de los desafíos anteriores.

1.4 Two candles

1:3: Una mancha en la mesa

1.2: Las palmeras y el pez

Hay una forma gráfica de resolverlo, a ver si das con ella. Se puede utilizar Geogebra.

1.1: Puzzle geométrico

Sin usar fracciones, encuentra, de forma razonada,  el valor del lado que está señalado.

Comenzamos el curso 15-16

Comenzamos con un problema del Calendario Matemático del mes de septiembre, al que puedes acceder desde el lateral.

Se ha dividido el rectángulo en 9 rectángulos. El número que aparece en alguno de ellos es la medida de su área. La pregunta es ¿Cuánto vale x?

35.- Diagonales

¿Cuántas diagonales tiene un polígono de 100 lados? No, no hace falta que las dibujemos y las contemos una a una. Para llegar a saber cuantas, sigue el camino que te indica la actividad de este enlace. Pertenece al proyecto Gauss.
Responde a las preguntas que se hacen en dicha actividad.

34.- Triángulos de área 1

Sobre la trama 5x5 que tienes aquí debajo, puedes mover los puntos amarillos para ir formando triángulos. Irás viendo el área y el perímetro de todos los que se van formando. Investiga para encontrar pautas que te permitan contestar a las preguntas que se formulan a continuación.



 Busca todos los triángulos de 1 unidad cuadrada de área, ¿cuántos has obtenido?
Dibuja todos los modelos distintos en una hoja.

33.- Día Escolar de las Matemáticas

La prensa ofrece muchas posibilidades de encontrar referencias a las matemáticas. Fíjate en algún ejemplo del blog que te enlazo que te sirva como modelo,. y elabora un comentario matemático de una noticia de cualquier periódico. Hay que poner la noticia, el enlace a la web de donde se ha sacado y el comentario matemático. Puedes incluir gráficos o dibujos tuyo que te sirvan para explicar lo que quieras decir.

http://mathsynews.blogspot.com.es/ 

32.- Capicúas

Todos los números de 4 cifras son divisibles por el mismo número. ¿Cuál? 

Explícalo razonadamente. Piensa en los criterios de divisibilidad.

¿Ocurre lo mismo con los capicúas de 5 cifras? ¿Y con los de seis cifras?

31.- Elementos

¿En qué ciudad nació el descubridor del elemento cuyo peso atómico es el resultado de esta ecuación?

30.- El seis

Si escribes todos los números impares entre el 55 y el 555,

   

¿cuántas veces habrás usado la cifra 6? 

Da una respuesta razonada

29.- El ciclista

Un ciclista sube un puerto a una velocidad de 8 Km/h. Y baja la misma distancia a 24 Km/h.

¿Cuál ha sido la media de velocidad en todo el recorrido?

28.- Año de nacimiento

Un matemático canadiense, que vivió en el siglo XIX, solía decir su edad con el siguiente acertijo:

El año x² tenía x años. ¿En qué año nací?

Calcula el año de nacimiento y quién es ese matemático

27.- Cinta de Moëbius

En la sección 1+1 de la programación local de Ondacero Calamocha, se habla de matemáticas cada semana. En el programa que enlazamos aquí se habla de la banda de Moëbius. Escúchala y contesta a las siguientes cuestiones que se plantean.  Pincha aquí para escucharlo

Sigue las indicaciones que se dan en el programa de radio y realiza las construcciones que se explican (esto hay que entregarlo). Cita en un comentario a este artículo dos utilidades de la cinta, que se nombran en el programa.

26. Dados

Las caras que se tocan en los dados de la izquierda, junto con la cara coloreada de rojo, esconden el día y el mes de una fecha, cuyo año se encuentra en las caras que se tocan de los dados de la derecha.

¿Para qué concepto introdujo un símbolo el matemático que nació siete meses después de esta fecha?

(Responde por medio de un comentario a esta entrada)

Eclipse

25.- Los perímetros

Problema de los días 16 y 17 de marzo del calendario matemático de la Sociedad Al-Kwarizmi

23.- Sol. Partidos de tenis

Un torneo de tenis se juega por el sistema de eliminación directa, que quiere decir que el perdedor de un partido queda eliminado del torneo. Si participan 128 jugadores,

¿cuántos partidos deberán disputarse para conocer el ganador? Razona la repuesta.

Todas las soluciones recibidas van contando cuantos partidos se van jugando en cada fase: Así en la primera eliminatoria serán 64, en la segunda, 32, 16 en la tercera, 8 en la siguiente, 4 a continuación, 2 en la semifinal y uno más para la final, en total 127.

Pero Ángela nos propone una solución distinta: Si hay 128 participantes y solamente puede ganar uno, 127 tienen que perder un partido, por lo cual se disputan 127 partidos.

24.- Rebajas, rebajas

Estamos en plena temporada de rebajas en los comercios. Ya se ven, o pronto se verán, los carteles de 2ª rebajas.
En dos tiendas cercanas A y B ya están en segundas rebajas y tienen una camisa al mismo precio las dos.
En la tienda A, costaba antes de las rebajas, 60€ y le han aplicado dos descuentos: un 20% en las primeras rebajas y al precio resultante un 50%.
En la tienda B han hecho un 70% de descuento pero sobre el precio original.

¿Cuánto costaba la camisa en la tienda B antes de las rebajas?

21.- Sol. Greguerías

Las greguerías son frases que muestran interpretaciones o comentarios ingeniosos y humorísticos sobre aspectos de la vida corriente. Fueron creadas y así denominadas por el escritor Ramón Gómez de la Serna (Madrid 1888 - Buenos Aires 1963).

 

La tertulia del café del Pombo. J. Gutiérrez Solana

Gómez de la Serna definió la greguería con la siguiente ecuación:

 HUMORISMO + METÁFORA = GREGUERÍA

Puedes encontrar muchas en Internet. El autor escribió más de diez mil. A nosotros, nos interesan aquellas que tienen que ver con las matemáticas. Y las hay.

Como actividad te propongo que pongas tu imaginación a funcionar para crear tus propias greguerías

Cada vez tenemos menos respuestas. En esta ocasión sólo una, de Álvaro:
Un rectángulo son dos sietes mirándose del revés y formando cuatro ángulos rectos 

22. Año por siglo

En esta ocasión deberás utilizar internet y poner en práctica tus dotes de investigador para resolver el desafío. La respuesta la pones en un comentario a esta entrada, pero no se verá hasta que no se acabe el plazo de entrega.

Concurso Fotografía Matemática

Estas son las fotografías presentadas para el concurso organizado en la Semana Matemática de nuestro centro. Sólo hemos tenido fotos de 3º y 4º, pero podrían haber sido muchas más.

20. Solución. Con regla y compás

El desafío de esta semana consiste en leer las instrucciones y  reproducirlas en un folio, a lápiz, utilizando la regla y el compás,  con limpieza y precisión. Una vez que esté completa, deberás reconocerla en el lugar del instituto en que se encuentra. El trabajo habrá concluido cuando la ubiquéis, reflejándolo por escrito debajo del dibujo. 

INSTRUCCIONES:

- Dibuja en una hoja un segmento MN de 16 cm.
- Marca el punto medio del segmento MN y llámale A.
- Con centro en A, dibuja una semicircunferencia de radio 8cm, que pasará por los puntos M y N.
- Levanta una recta perpendicular a MN en el punto A hasta que corte a la semicircunferencia en un punto que denotaremos B.
- Busca el punto medio del segmento AB y llámalo C.
- Construye la circunferencia de centro C y radio la distancia de C a A (que será 4cm).
- Busca el punto medio del segmento MA y traza la semicircunferencia con centro allí y radio hasta M (que será 4cm). Observa que dicha semicircunferencia corta a la circunferencia central en un punto que llamarás P.
- Busca el punto medio del segmento NA y traza la semicircunferencia con centro allí y radio hasta N (que será 4cm). Observa que dicha semicircunferencia corta a la circunferencia central en un punto que llamarás Q.
- Por último, pinta la superficie con vértices A y P, la de vértices A y Q, la de vértices M, P y B, y la de vértices A, N y B.

¡ÁNIMO Y A DIBUJAR!

¿Dónde se encuentra en el instituto?

He recibido cuatro dibujos. El que pongo aquí es el de Andrea Cebrián.

18.- Solución El andarín

Un andarín infatigable y alto (2 metros) se propone dar la vuelta al mundo andando. Tras mucho buscar encuentra un artilugio que le permite desplazarse por toda la superficie del planeta, incluso por encima de las aguas. Con muchos esfuerzos logra su hazaña, y en la nebulosa de su cansancio una pregunta que no sabe responder no le deja descansar:

¿Cuántos kilómetros más ha recorrido mi cabeza que mis pies?

En esta ocasión solo he recibido tres respuestas, todas correctas. Pongo aquí la de Lorena.

19.- Cuentos

Seguro que sabes el cuento de la liebre y la tortuga. Aquí tienes una gráfica que cuenta cómo podría haberse desarrollado la carrera.

La tarea para esta semana es que escribas el cuento adaptándote a la gráfica anterior. O si lo prefieres, puedes hacer la gráfica de otro cuento.

17.- Refranes

En nuestra vida cotidiana utilizamos muchas veces los refranes. En ellos se relacionan conceptos distintos, y cuando eso ocurre, hemos aprendido que se pueden visualizar a través de una gráfica.
La propuesta de esta semana, aunque te parezca extraña, es que hagas la representación gráfica de un refrán.
Tendrás que elegirlo fijándote en que relacione dos variables. En unos ejes coloca las variables y la magnitud con las que las vas a medir. Y ya puedes hacer la gráfica.

Aquí van algunos de los recibidos:

Hypatia

Amenábar la hizo protagonista de su película Ágora. Nació hacia el año 370 en Alejandría, Egipto. Es la primera mujer de ciencia cuya vida está bien documentada. Puedes leer más sobre su vida en este enlace.
En el calendario que tienes en el menú de la izquierda de este blog, el día 18 de enero, hoy, recoge una máxima de esta mujer, sobre la que te invito a reflexionar y poner en práctica:

“Conserva celosamente tu derecho a reflexionar, porque incluso el hecho de pensar erróneamente es mejor que no pensar en absoluto”